Dr. Glen Brown
Global Accountancy Institute, Inc. and Global Financial Engineering, Inc.

Abstract

In the evolving field of financial engineering, integrating adaptive risk management with technical market analysis is key to constructing a robust and efficient trading system. This article introduces our novel Adaptive Volatility Scaling Principle (AVSP), which enhances the traditional square root of time rule by incorporating market phase information from our Color-Coded EMA Zones. By defining the Global Adaptive Time Scaling Factor (GATSF) as the square root of PPP, where PPP represents the period derived from specific technical boundaries, we create a dynamic framework to adjust trailing stops (via DAATS) and break-even triggers (through our GASBET Model). This approach bridges rigorous statistical principles with insightful technical analysis, ultimately optimizing trade exits and improving risk-adjusted returns.

1. Introduction

Financial markets are inherently volatile, and successful trading hinges on dynamic, adaptive risk management. Our proprietary Global Algorithmic Trading Software (GATS) Framework is built on the foundation of quantitative research, systematic trading, and adaptive risk controls. A key component is the Dynamic Adaptive ATR Trailing Stop (DAATS), whose calculation depends critically on market volatility. Traditionally, volatility is scaled using the square root of time—a method that serves as the backbone of many quantitative risk management models. In our system, we refine this approach by selecting the period PPP from technical benchmarks provided by our Color-Coded EMA Zones, thereby integrating the Adaptive Volatility Scaling Principle (AVSP) into our risk management framework.

2. The Square Root of Time Principle and Its Role in GATSF

2.1 The Classic Concept

The square root of time rule is a well-established principle in financial statistics. It posits that if individual price fluctuations are independent and identically distributed, the standard deviation (or volatility) over PPP periods scales as:

3. Adaptive Volatility Scaling Principle (AVSP)

3.1 Conceptual Foundation

We propose the Adaptive Volatility Scaling Principle (AVSP) as an extension of the classic square root of time rule. AVSP posits that the effective volatility over a trading session is not only a function of the passage of time but is also significantly influenced by the market phase. By using technical indicators—specifically, our Color-Coded EMA Zones—to select PPP, we ground our volatility measurement in the market’s actual behavior.

3.2 Practical Implementation

• Choosing PPP from Technical Boundaries:
  Instead of referencing a generic period (like a full trading day), we select PPP from the boundaries of our EMA zones. For instance, using the upper boundary of the Transition Zone (EMA 25) provides P=25, leading to a GATSF of 5.
• Integration with DAATS:
  The DAATS formula becomes:

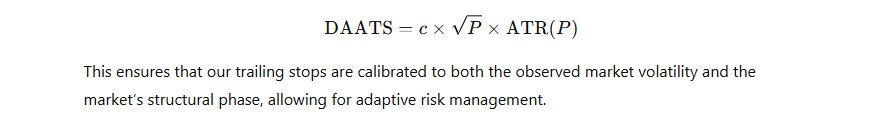
3.3 Impact on Risk Management

By aligning our volatility scaling with market phases:

• Contextual Trailing Stops:
  Our stops widen or tighten based not just on volatility, but also on the technical environment. For example, during a transition phase indicated by EMA 25, our stops will be set according to a PPP that reflects that specific market structure.
• Improved Exit Strategies:
  This approach feeds into our Global Adaptive Statistical Break-Even Trigger (GASBET) Model, which uses statistical measures—like the mean and standard deviation of DAATS—to set dynamic break-even triggers. The combined effect ensures that profits are secured only after statistically significant moves, enhancing overall risk-adjusted performance.

5. Conclusion

The Adaptive Volatility Scaling Principle (AVSP) and its integration into our GASBET Model represent a significant advancement in adaptive risk management. By selecting the ATR period PPP based on key technical indicators—such as the upper boundary of the Transition Zone in our Color-Coded EMA system—we create a Global Adaptive Time Scaling Factor (GATSF = P\sqrt{P}P​) that accurately reflects market conditions. This approach, combined with our dynamic DAATS calculation, allows our system to adjust trailing stops and break-even triggers in a statistically robust and market-responsive manner.

In doing so, we enhance our ability to secure profits dynamically while maintaining consistent risk controls, ultimately driving our proprietary trading strategies toward superior, risk-adjusted returns. This theoretical framework not only solidifies our methodology but also paves the way for continued innovation in financial engineering.

About the Author

Dr. Glen Brown is a pioneer in financial engineering and algorithmic trading. With decades of experience bridging academic theory with practical applications, Dr. Brown is the visionary founder of Global Accountancy Institute, Inc. and Global Financial Engineering, Inc. His innovative approaches—embodied in the proprietary Global Algorithmic Trading Software (GATS) Framework—have set new industry standards in adaptive risk management and systematic trading. Dr. Brown’s work continues to drive breakthroughs in quantitative research, dynamic market analysis, and robust trading system design, positioning his organizations at the forefront of global financial innovation.

General Disclaimer

The information presented in this document is for educational and informational purposes only and should not be construed as investment advice. Trading in financial markets involves risk, and past performance is not indicative of future results. Readers are encouraged to conduct their own research and consult with a qualified financial advisor before making any investment decisions.

Global Accountancy Institute, Inc. and Global Financial Engineering, Inc. operate as closed proprietary firms. We do not offer any products or services to the general public, nor do we accept clients or external funds. All methodologies, including the GATS Framework and its associated risk management models, are exclusively developed and used internally as part of our proprietary trading systems.

Neither Dr. Glen Brown nor his affiliated institutions accept any responsibility for any loss or damage incurred as a result of the use or application of the information provided.